Die moderne Physik ist auf der Suche nach der Weltformel. Sie möchte das, „was die Welt im Innersten zusammenhält“ in einer Formel greifen. Der Harmoniker ist etwas bescheidener. Er legt sich auch nicht auf ein Einziges fest. Er sucht, sich dem gemeinsamen Band anzunähern, das „jede Figur, jede Zahlenverbindung, das ganze System der Harmonie und den Umlauf der Gestirne“ miteinander verbindet, wie es Platon (ca. 428–348 v. Chr.) ausdrückte. Vier Aspekte haben wir hier. Mit den Figuren sind dabei die geometrischen gemeint, mit dem System der Harmonie die musikalischen Intervalle und ihre Ordnung. Wir können auch den von Pythagoras (ca. 580–500 v. Chr.) geprägten Begriff der Sphärenharmonie – in einem weit gefassten Sinne – verwenden.
Sphärenharmonie ist nicht tönende Musik, aber sie hat mit Musik zu tun, genauer: mit deren Aufbau. Sphärenharmonie hat auch mit dem Kosmischen zu tun, aber beschränkt sich nicht auf das unerreichbare Weltall. Sie hat auch mit Mathematik zu tun, mit deren beiden Seiten; zum einen der abstrakten, also den Zahlen und dem Berechnen, zum anderen mit der konkreteren, anschaulicheren Seite, der Geometrie. Die vier weiter oben genannten Aspekte Zahl, Geometrie, Grundlagen der Musik und Astronomie wurden im Mittelalter zusammen als sogenanntes „Quadrivium“ an den Universitäten gelehrt. Auch für den heutigen Harmoniker sind die vier Bereiche gleichberechtigt, auch wenn der ein oder andere von ihnen einen besonderen Schwerpunkt setzt.
Archetypen der Schöpfung
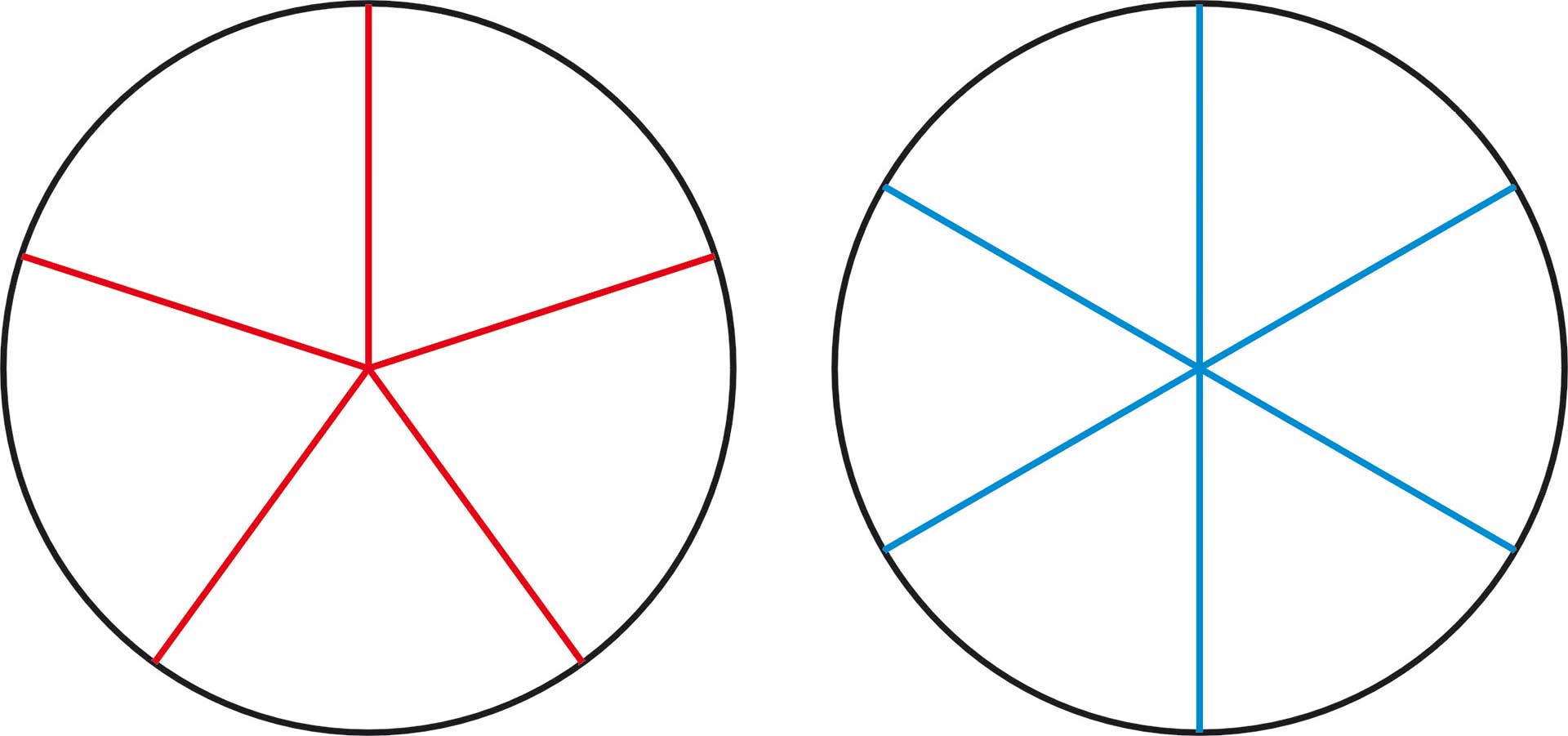
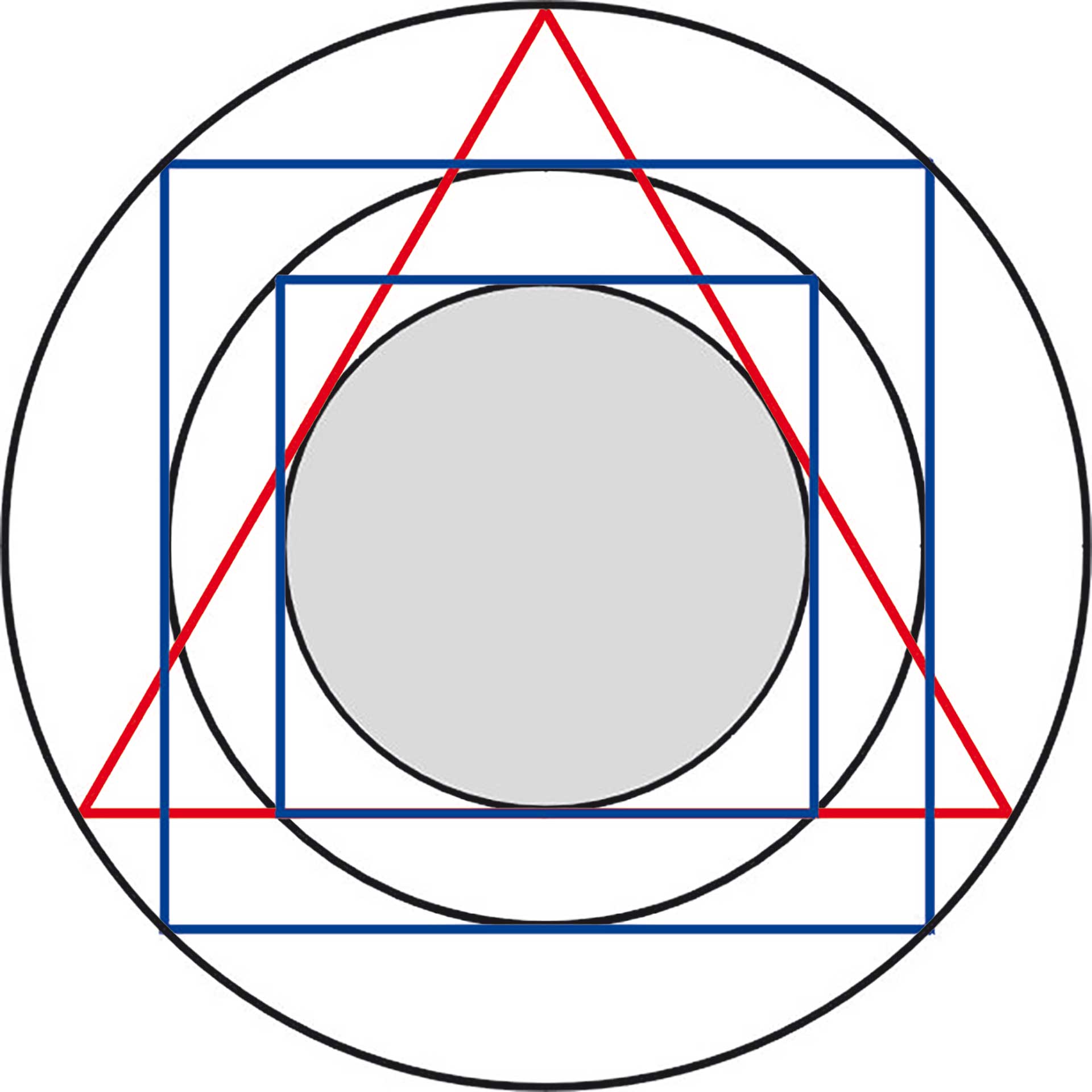
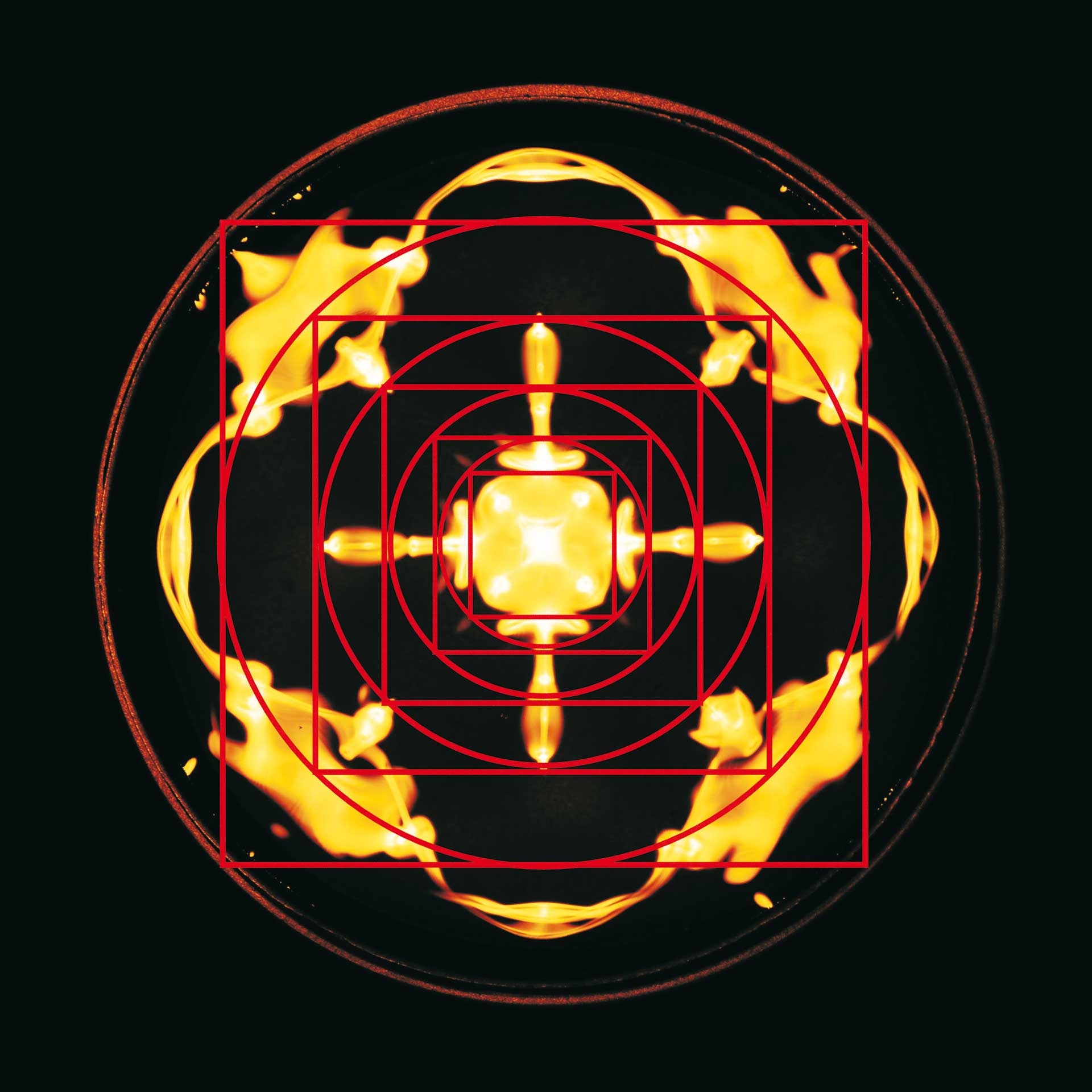
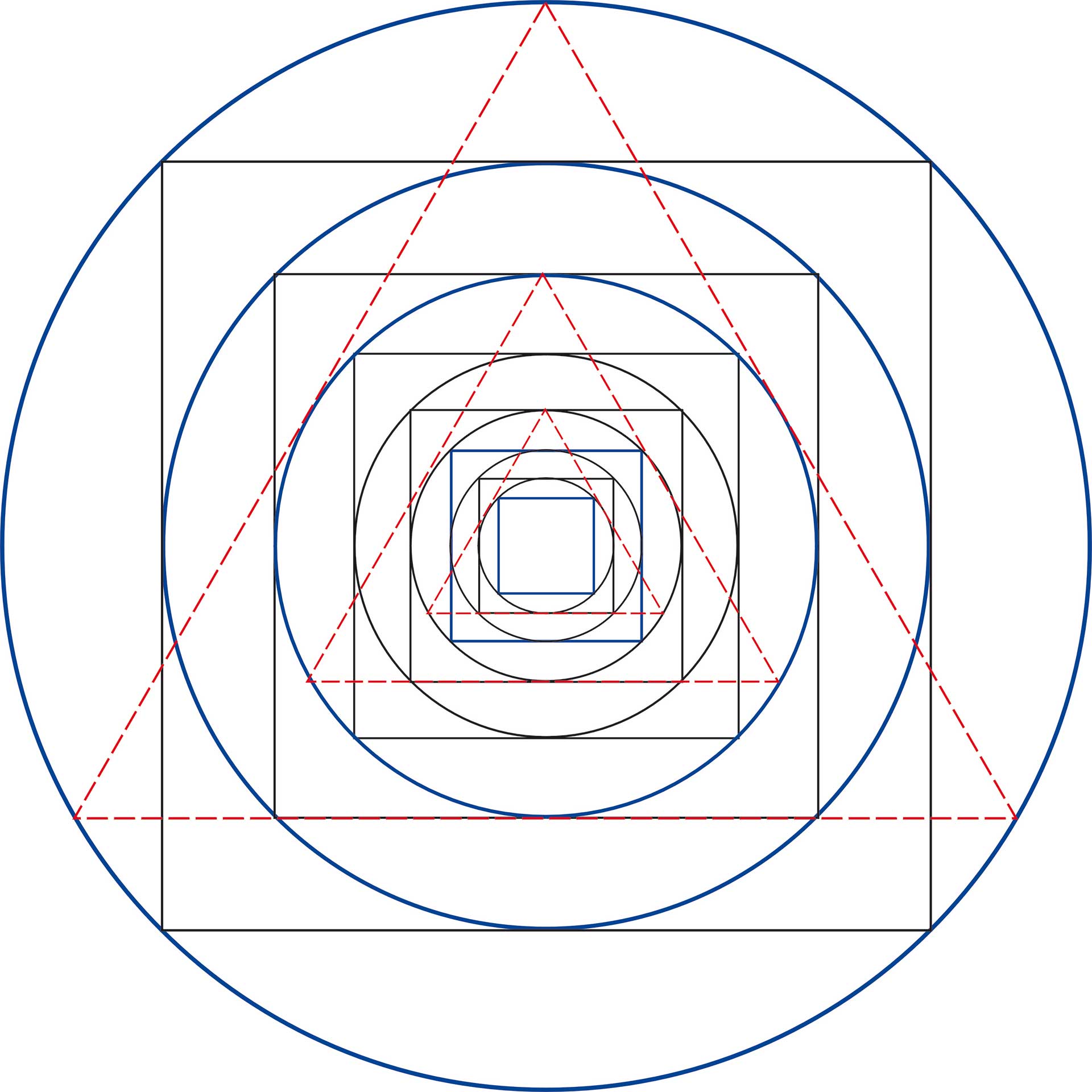
Für einen der größten Astronomen und Harmoniker, Johannes Kepler (1571–1630), den Entdecker der fundamentalen Bewegungsgesetze der Planeten, spielte nicht die Astronomie, sondern die Geometrie die Hauptrolle. Die Geometrie, so Kepler, lieferte „Gott die Urbilder (oder Archetypen) für die Schöpfung.“ Diese geistigen Urbilder geben den konkreten Erscheinungen in der materiellen Welt die Form, besser: das Gerüst der Gestalt. Den Ausdruck „konkrete Erscheinungen in der materiellen Welt“ müssen wir im weitesten Sinn auffassen. Sehen wir uns nun drei Bespiele für Formen in der Natur, ebenfalls im weitesten Sinne, an (Abb. 1).
Planetarische Bewegungsfiguren, kurz Planetenbilder, bilden sich, indem ihre in Beziehung gesetzten Bewegungen über Zeiträume von Jahren bis Jahrtausenden (je nach beteiligten Planeten, die äußeren laufen sehr langsam) aufgetragen werden. Dies geschieht in der Ebene der Ekliptik, das schmale Band, in dem die Planeten um die Sonne laufen. Wir haben in den Planetenbildern also Raum-und-Zeit-Abbildungen. Wasserklangbilder entstehen, indem Wasser auf eine schwingungsfähige Membran gebracht und diese mit einem Klang oder einer Sinusschwingung angeregt wird. Was wir sehen, ist eine Momentaufnahme in einem Schwingungsvorgang. Durch Licht wird dieser sichtbar gemacht. Nur bei der Blüte haben wir tatsächlich eine feste „materielle Erscheinung“.
Was ist nun das Gemeinsame der drei Bilder – Wasserklangbild, Blume, Planetenfigur – aus Abb. 1? Zunächst stellen wir fest, dass die drei Bilder nach der gleichen Zahl geordnet sind. Doch ist dies eine recht grobe Aussage, die die feineren Merkmale der Strukturen nicht berücksichtigt.
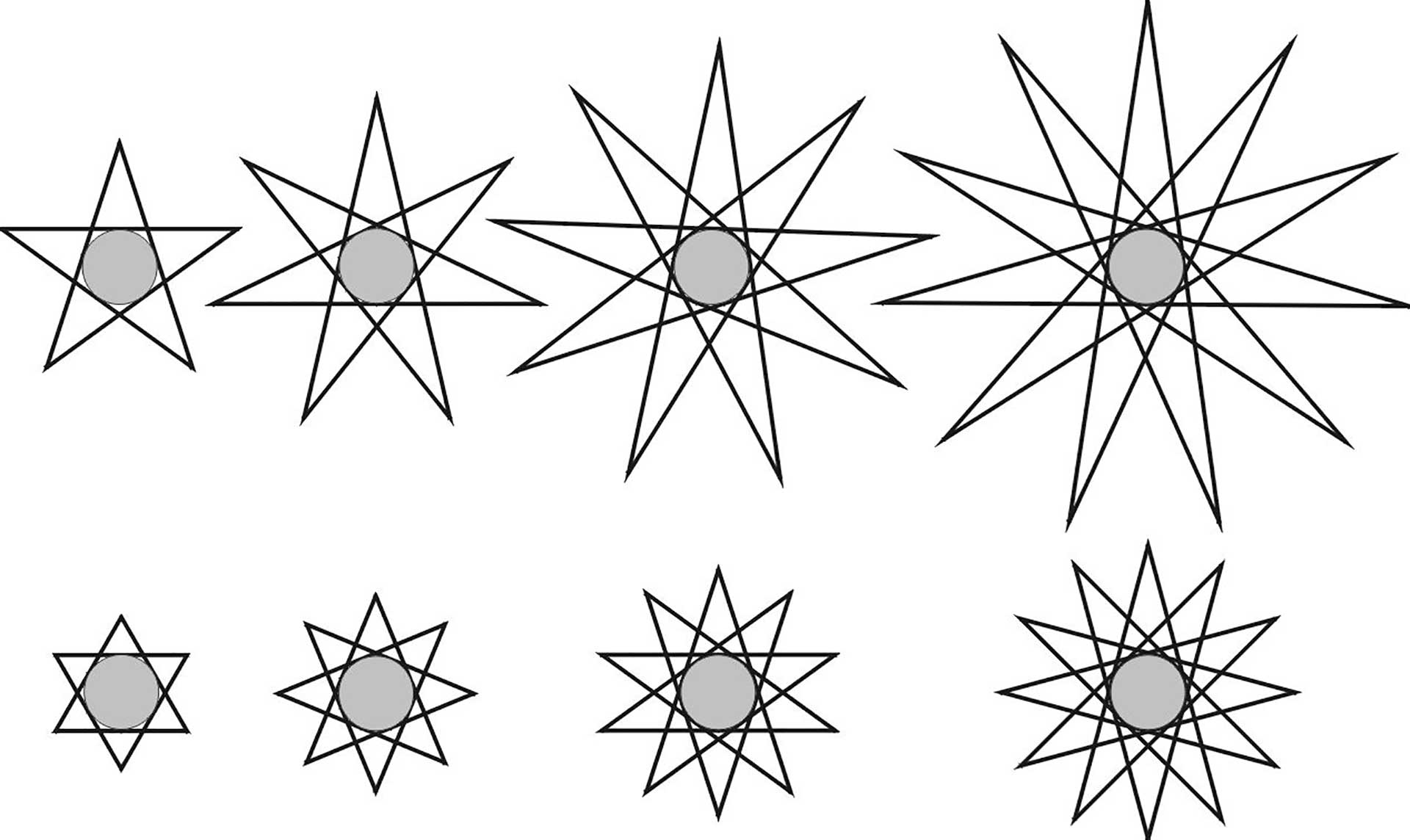
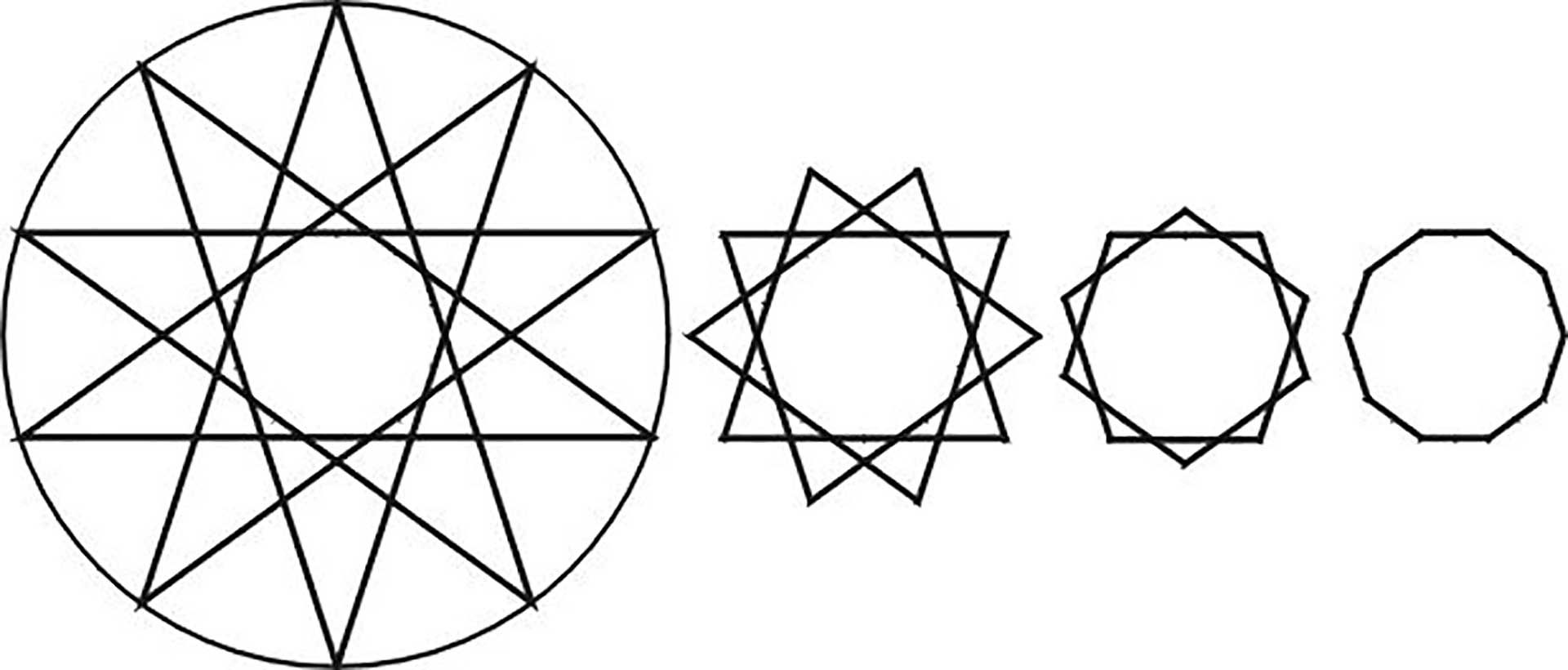
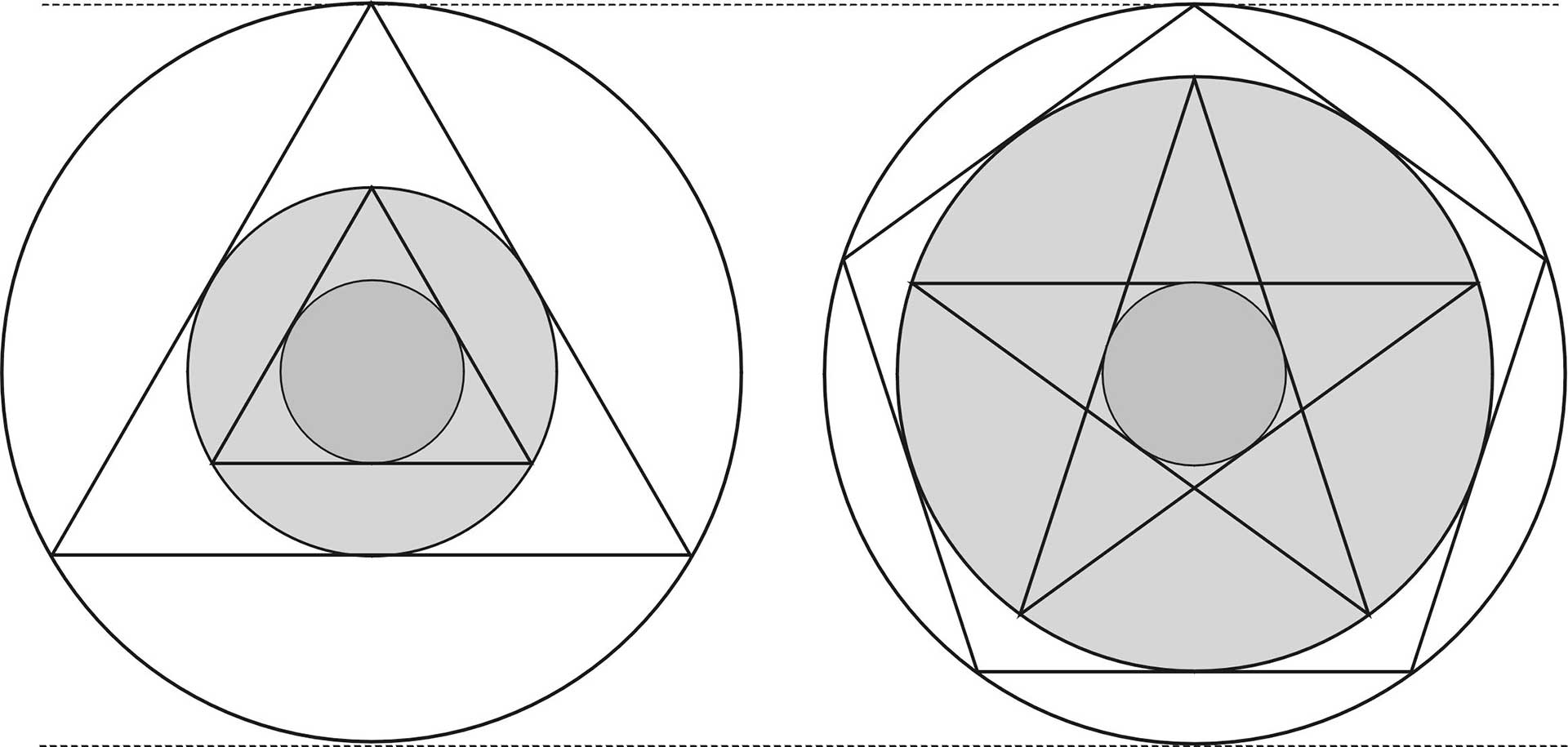
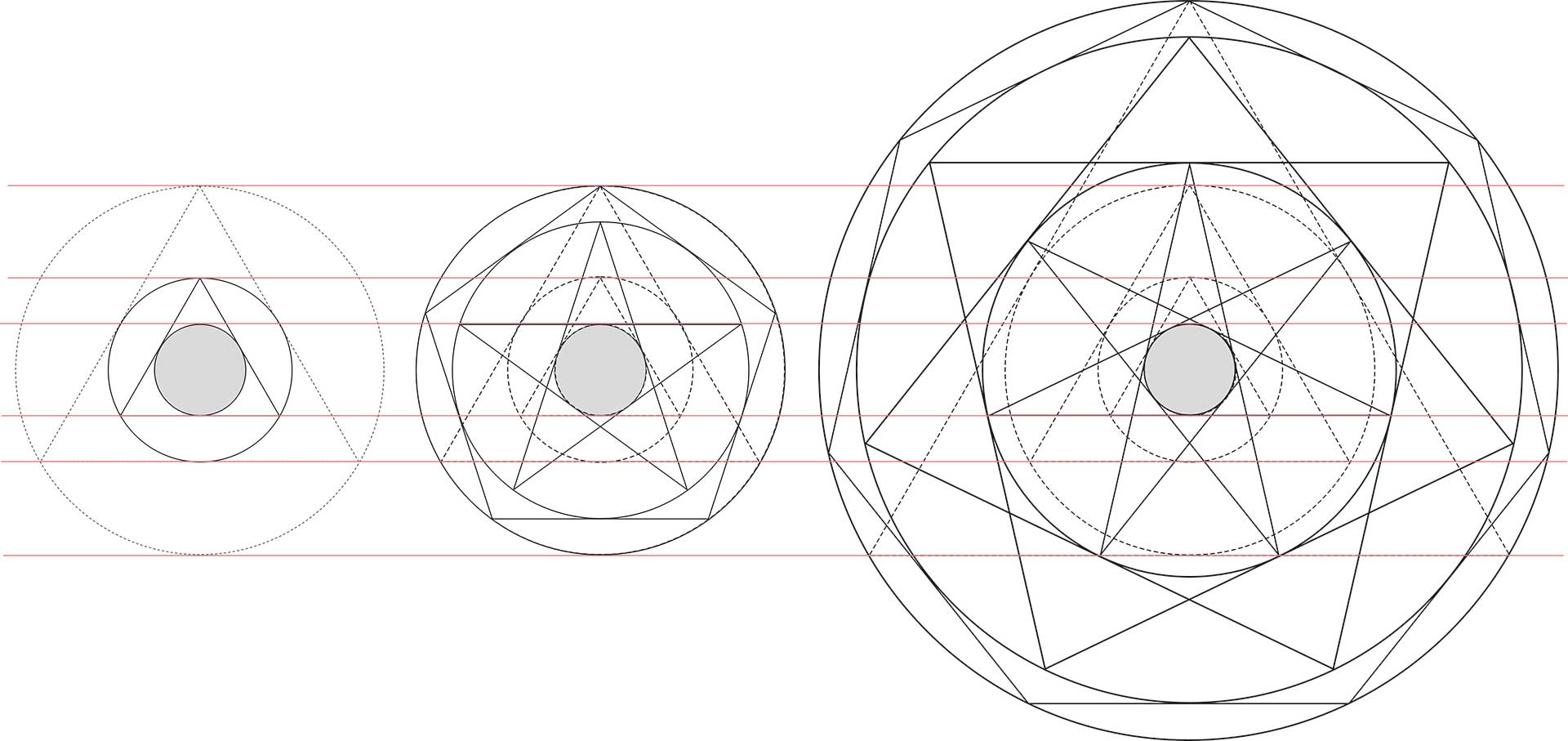
Johannes Kepler sprach, wie erwähnt in seiner Welt-Harmonik von geome-
trischen Urbildern oder Archetypen, die verschiedenen Bereichen der Schöpfung zugrunde liegen. Dies waren für ihn vor allem Polygone (= Eckfiguren), also Dreieck, Viereck, Fünfeck, Sechseck und ein paar andere. Diese Vorstellung konnte ich in den Untersuchungen, die zum Buch „Der Sternenorganismus“ geführt haben, erweitern. Die hauptsächlichen geometrischen Urbilder sind die Sternfiguren. Und diese umfassen auch die Polygone. Denn jeder gezeichnete Stern trägt im Inneren die entsprechende Eckfigur. Zum Beispiel zeichnet das Pentagramm im Inneren ein Fünfeck, das Hexagramm ein Sechseck usw.