In den raum&zeit Ausgaben Nr. 219 und 220 wurde der Oktavaufbau der Zahlen mit seinen fundamentalen Wellenlängen vorgestellt. Bestätigt durch die erstmalige Entdeckung des selbstähnlichen Oktavenmusters der Zahlen wurde des weiteren deutlich, dass die Ersten Zahlen (Primzahlen) auf den Oktavaufbau der Zahlen hinweisen bzw. auf die
sen zurückzuführen sind. Die darauffolgenden Ausgaben 221 und 222 von raum&zeit zeigten, dass der Oktavaufbau auch für die Entstehung der Eulerschen Zahl e, der Kreiszahl π und des Goldenen Schnitts φ sowie für das harmonische Widerklangverhältnis (Resonanzverhältnis) von Elektron und Proton ursächlich ist. Schließlich lieferte sogar das Auftauchen der Wallis-Formel für π in der Berechnung der Anregungszustände des Wasserstoffatoms einen quantenphysikalischen Beweis für den Oktavaufbau. 1 So ergaben sich erste Hinweise, Zusammenhänge zwischen Oktav- und Atomaufbau zu suchen. Das Gleichbleiben der Wellenlängen des Oktavaufbaus der natürlichen Zahlen erlaubte zudem den Rückschluss auf eine stehende Welle als Ursprung; dieser Ursprung ist ein Urklang. In der Folge konnte erkannt werden, dass Zahlen nichts anderes als Widerklangverhältnisse zu diesem Urklang darstellen. So darf im vorliegenden Artikel ein Schritt weitergegangen und gezeigt werden, dass der Oktav-aufbau der Zahlen sogar eine Herleitung der dreidimensionalen Form von Atomen erlaubt. Aus dem Erkennen der wirklichen Gestalt des atomaren Aufbaus ergeben sich neue Möglichkeiten der Anwendung, die Thema des zweiten Teils sein werden.
Aufbau der Atome
Zahlen und der in ihnen angelegte musikalische Oktavaufbau sind Ausdruck der universellen
Ordnung. Diese durchzieht gleichmäßig alle großen und kleinen Maßstäbe. Matthias Pauqué, der mit seiner nun „Universelle Gleichmäßigkeit“ genannten Theorie Hartmut Müllers „Global Scaling“ erweitert hat, beleuchtet hier in Teil 1 seines Artikels den Mikrokosmos der Atome. Erlaubt bereits der
Oktavaufbau der Zahlen Rückschlüsse auf die atomare Gestalt?
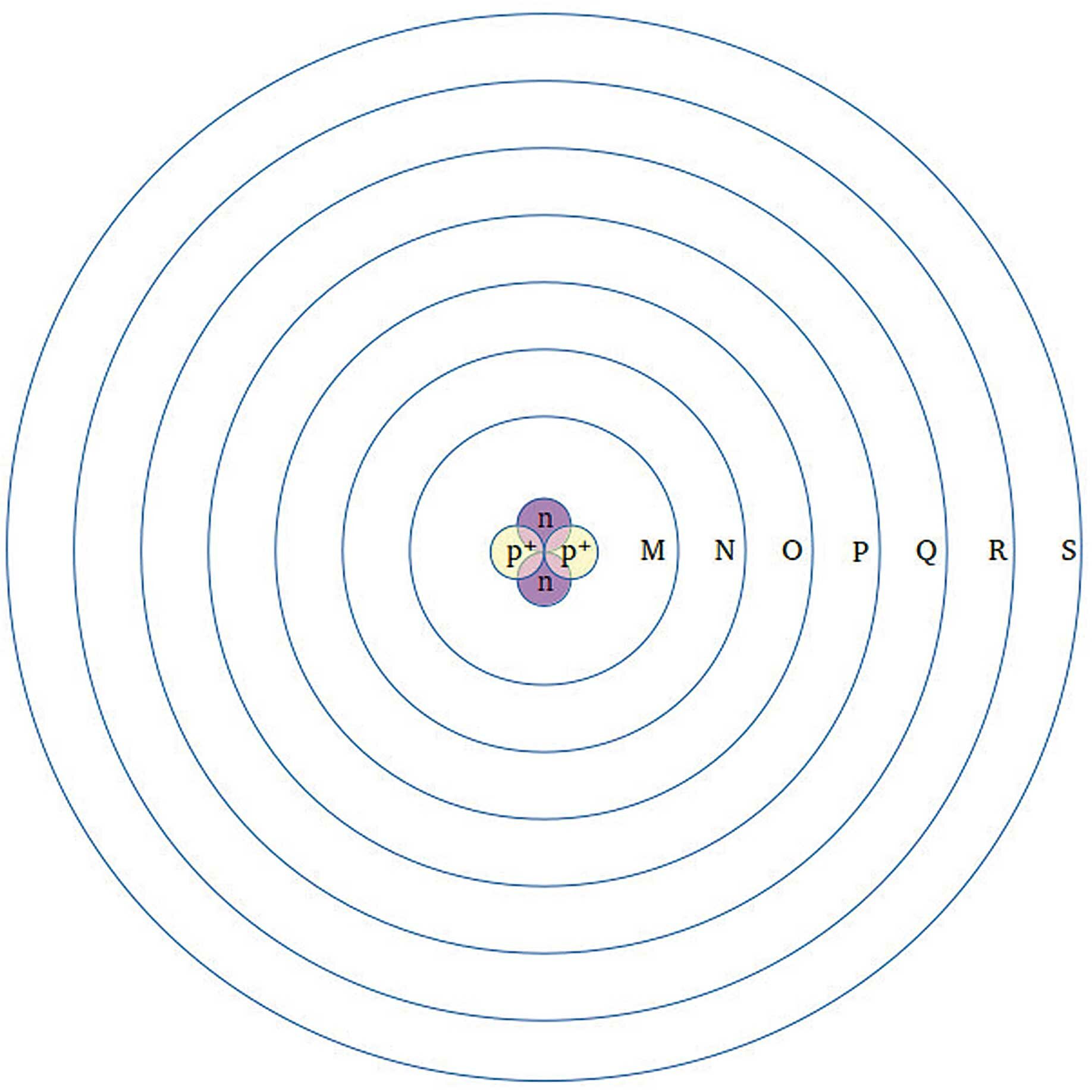

Das Bohrsche Modell
Wie wirken die Gegebenheiten des Oktavaufbaus nun in den atomaren Aufbau hinein? Dazu sei zunächst ein Blick auf die heute herrschende Vorstellung vom Atomaufbau geworfen. Es ist immer noch im Wesentlichen der Ansatz von Niels Bohr, anhand dessen man Atome beschreibt. Zwar gibt es theoretische Erweiterungen dazu, um gewisse Eigenschaften beschreibend zu erfassen, jedoch führte dies zu keinem in sich schlüssigen Gesamtbild. Die gegenwärtige Vorstellung vom atomaren Aufbau spricht von einem Atomkern, bestehend aus Protonen und Neutronen, und sogenannten Schalen, auf denen sich die Elektronen wie Planeten eines Sonnensystems bewegen (Abb. 1). Bis heute kann man sich zum Beispiel nicht erklären, warum sich nach Bohrs Vorstellung mehrere positiv geladene Protonen im Atomkern zusammenballen und nicht auseinanderfliegen. Man postuliert deshalb eine von allem anderen abweichende Gesetzmäßigkeit, die nur im Atomkern gelten soll, anstatt das gesamte Atommodell zu überdenken.
Die Vorstellung, dass Atome einem Sonnensystem gleich aufgebaut sind, ist aber nicht abwegig. Es entspricht der selbstähnlichen Denkweise, dasselbe Aufbauprinzip auf unterschiedlichen maßstäblichen Ebenen anzutreffen. Anhand der Erklärungsprobleme einiger Phänomene auf atomarer Ebene wird jedoch deutlich, dass das grundlegende Prinzip, das tatsächlich auf allen maßstäblichen Ebenen zur Anwendung kommt, noch nicht vollständig begriffen wurde.
Scaling des Schalenaufbaus
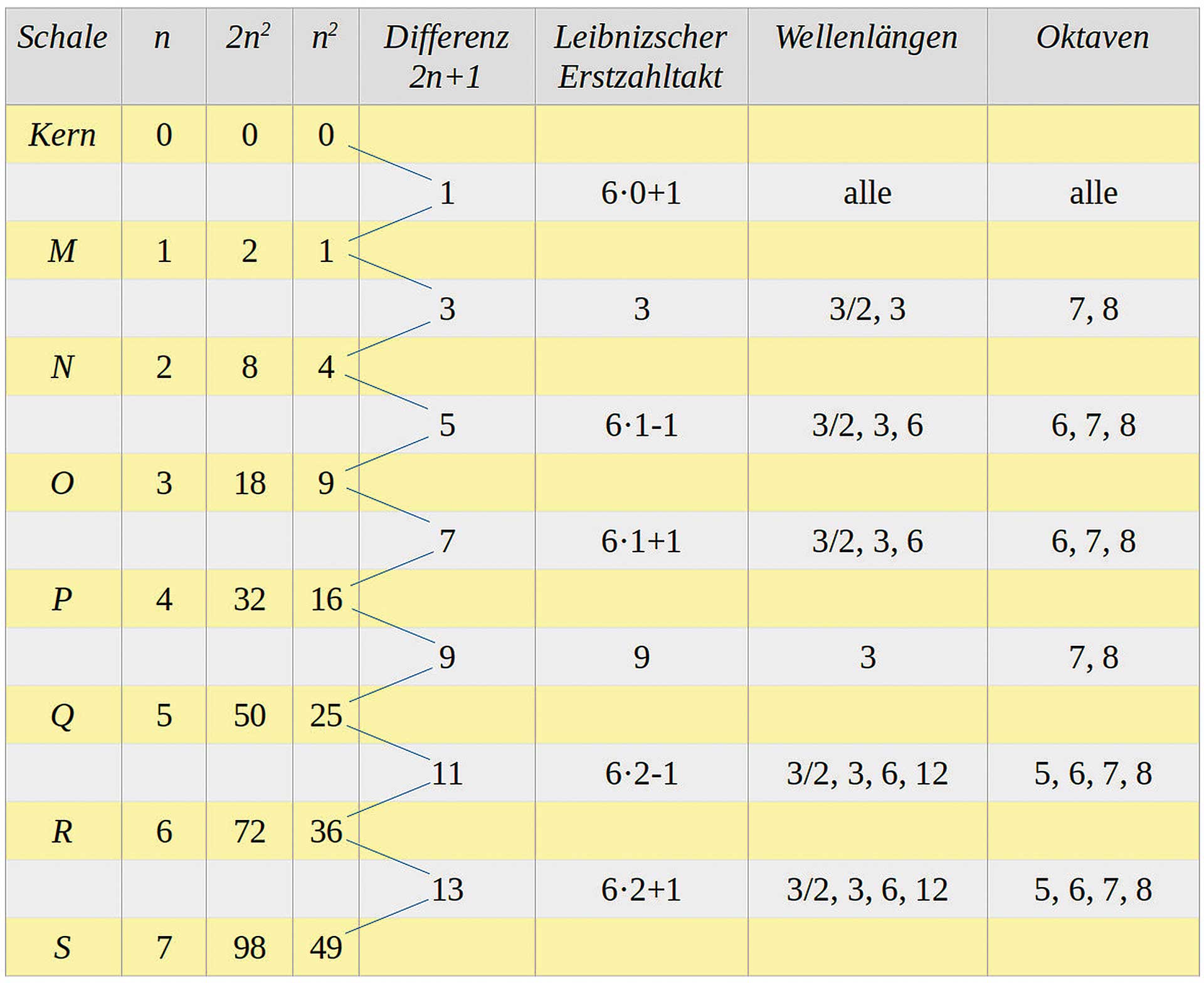
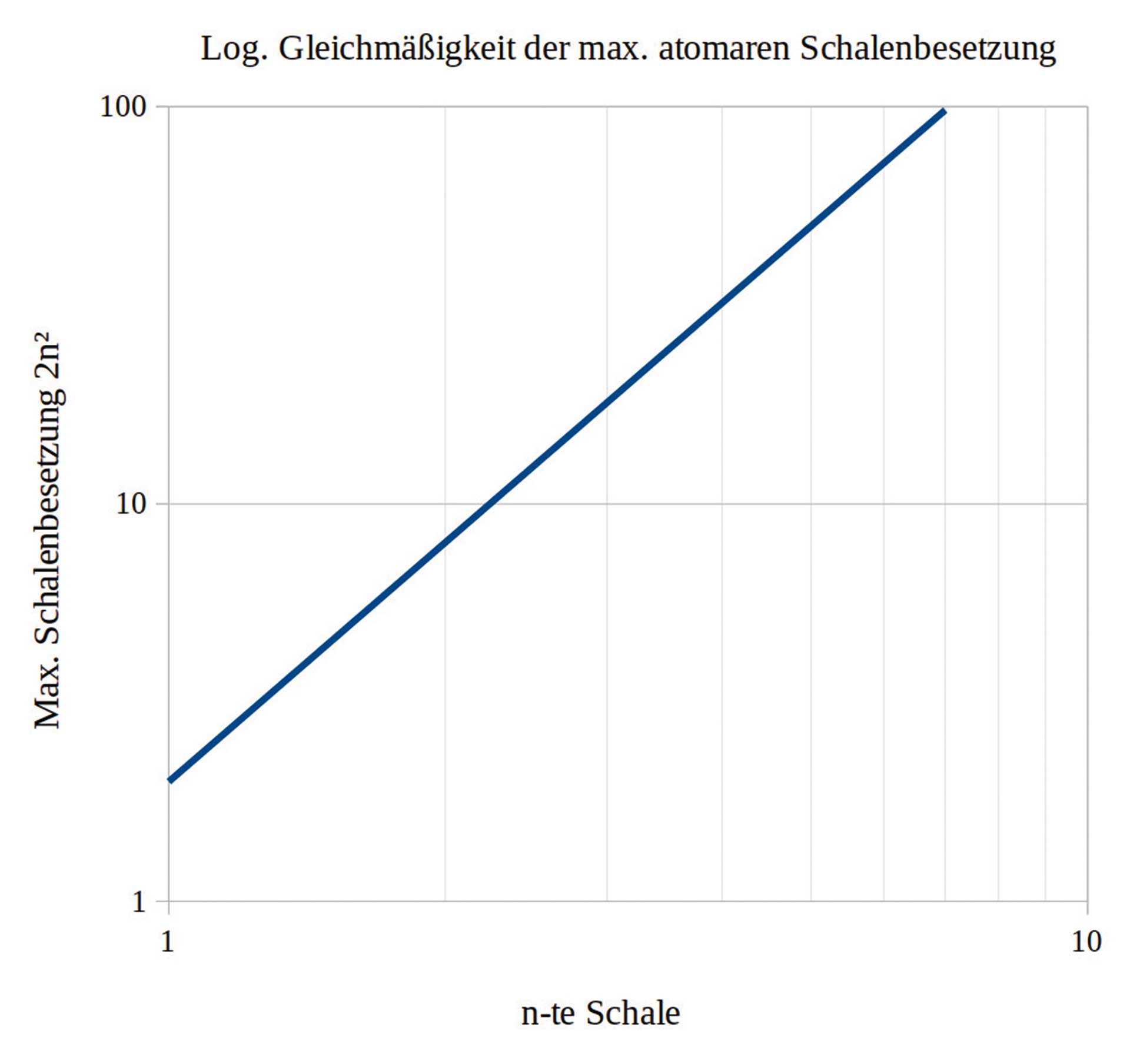
Zunächst verweilen wir jedoch beim Bohrschen Atommodell, um die logarithmische Gleichmäßigkeit (Scaling) des Schalenaufbaus zu erfassen. Zur Betrachtung der gequantelten Energieportionen in Vielfachen von Elektronen ist das Schalenmodell ausreichend, das Bohrsche Gesetz der Schalenbesetzung liefert in der Atomphysik zuverlässig richtige Ergebnisse. Wurde in raum&zeit Nr. 222 schon kurz auf die logarithmische Gleichmäßigkeit des Schalenaufbaus hingewiesen, wird diese jetzt genauer betrachtet. In Schale n mit n = 1, 2, …, 7 finden sich maximal 2n2 Elektronen, also bspw. in Schale fünf (Q, Abb. 1) maximal 50. Logarithmische Gleichmäßigkeit ist im Verhältnis der Menge n der Schalen und der maximalen Menge 2n2 an Elektronen je Schale erkennbar (Tab. 1 und Abb. 2).
Wo ist im 2n2-Gesetz der Oktavaufbau zu erkennen? Die Vervielfältigung um 2 zeigt einen Oktavsprung. Beim Quadrieren der Anzahl der Schalen n ist der Oktavaufbau indirekt beteiligt:
Die Differenz der Quadrate führt zur Folge der ungeraden Zahlen. Dazu werden die Differenzen der maximalen Elektronenanzahl je Schale (und damit indirekt die Differenzen der Quadratzahlen) betrachtet (Tab. 1). Diese beträgt 2(2n+1), also immer das Doppelte einer ungeraden Zahl.
Wie in raum&zeit Nr. 219 und 221 festgestellt, liegt den ungeraden Zahlen der Leibnizsche Erstzahltakt 6n±1 und dessen höhere Oktaven mit den Wellenlängen 3/2 und 3 zu Grunde. Die hier vorliegende Verdopplung der ungeraden Zahlen zeigt einen Oktavsprung an und weist ein weiteres Mal auf oktavenbegründete Widerklangverhältnisse hin.
Das 2n2-Gesetz verdeutlicht, dass man es im Atomaufbau hinsichtlich der Elektronenanordnung mit diskreten Werten zu tun hat. Ein Elektron ist die Grundeinheit, weitere Zustände sind ganzzahlige Vielfache. Das Auftreten diskreter Werte gab der Quantenphysik ihren Namen. 2 Ob zum Beispiel Energie oder Ladung – diese Größen treten in bestimmten Mengen als ganzzahlige Vielfache einer Basisenergiemenge oder -ladung auf. Das Auftreten logarithmischer Gleichmäßigkeit im Atomaufbau als selbstähnliche Wiederholung war an dieser Stelle wichtig festzuhalten.
Zurück zum atomaren Aufbau.
Selbstähnlichkeit
Neben der überall anzutreffenden logarithmischen Gleichmäßigkeit im Aufbau des Universums ist auch überall ein selbstähnlicher Aufbau zu finden. Warum sollte nun gerade im Atomkern ein anderes Gesetz herrschen, das plötzlich Protonen und Neutronen als separate Einheiten aneinanderdrängt (Abb. 1)? Hier eine abweichende Gesetzmäßigkeit zu postulieren, kann nicht folgerichtig sein. Die bislang gewonnenen Erkenntnisse sollen nun dazu herangezogen werden, eine vollständigere Vorstellung vom Atomaufbau zu entwickeln.Wie gelingt eine Verknüpfung des Oktavaufbaus der Zahlen mit dem Atomaufbau?
•Die herausragende Eigenschaft der Zahlen, in einer Welt der Verände-
rung gleich zu bleiben, erlaubte den Rückschluss auf eine stehende
Welle als Ursprung.
•Eine stehende Welle kann nur in einem begrenzten Medium ent- und bestehen. Die Annahme einer stehenden Welle in einem unbegrenzten Raum führte wiederum zu dem Schluss, dass es einen kreisförmigen Abschluss geben muss, weil so eine
Selbstbegrenzung gelingt. Übrigens konnte durch diese Erkenntnis auf Basis der Oktavordnung die Größe des Universums hinsichtlich eines kleinsten und größten Maßstabes bestimmt werden. 3
•Hinzu kommt die Eigenschaft der
Selbstähnlichkeit, die ausnahmslos überall anzutreffen ist. Die Wiederholung ein- und desselben Prinzips auf unterschiedlichen maßstäblichen Ebenen ist Ausdruck der Selbstähnlichkeit und der logarithmischen bzw. Universellen Gleichmäßigkeit (Universal Scaling).
Der Autor konnte dazu zeigen, dass die Eulersche Zahl e als universelle Maßzahl Ausdruck der universellen Selbstähnlichkeit beziehungsweise aller selbstähnlichen Wiederholung ist und sogar bereits allen arithmetischen Operationen zu Grunde liegt. 4
So ergibt sich die Annahme, dass sich diese Gegebenheiten auch im Atomaufbau finden lassen müssen. Wie bei allem anderen muss auch das Atom ein selbstähnliches Abbild dieser fundamentalen Gesetzmäßigkeiten sein.
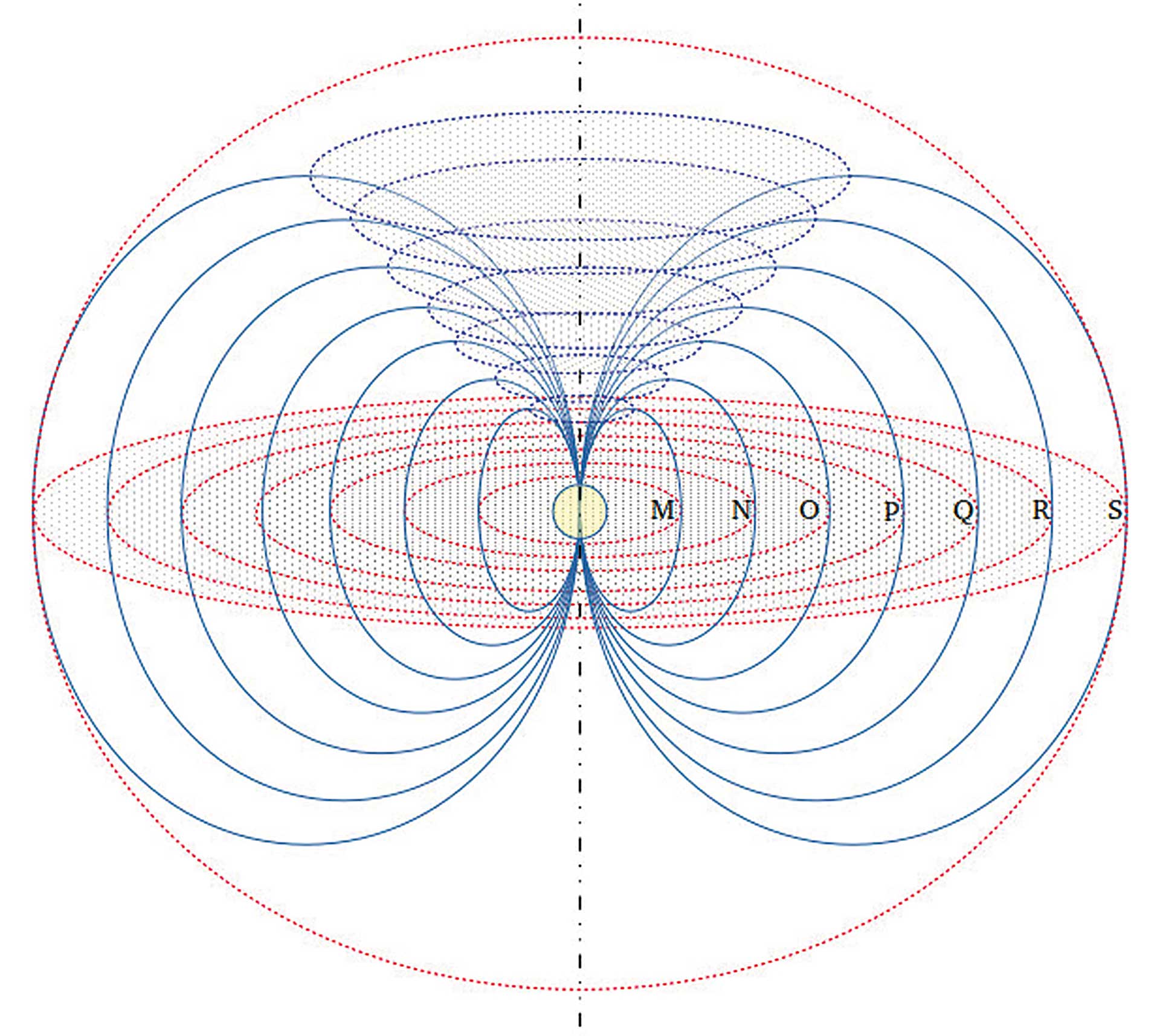
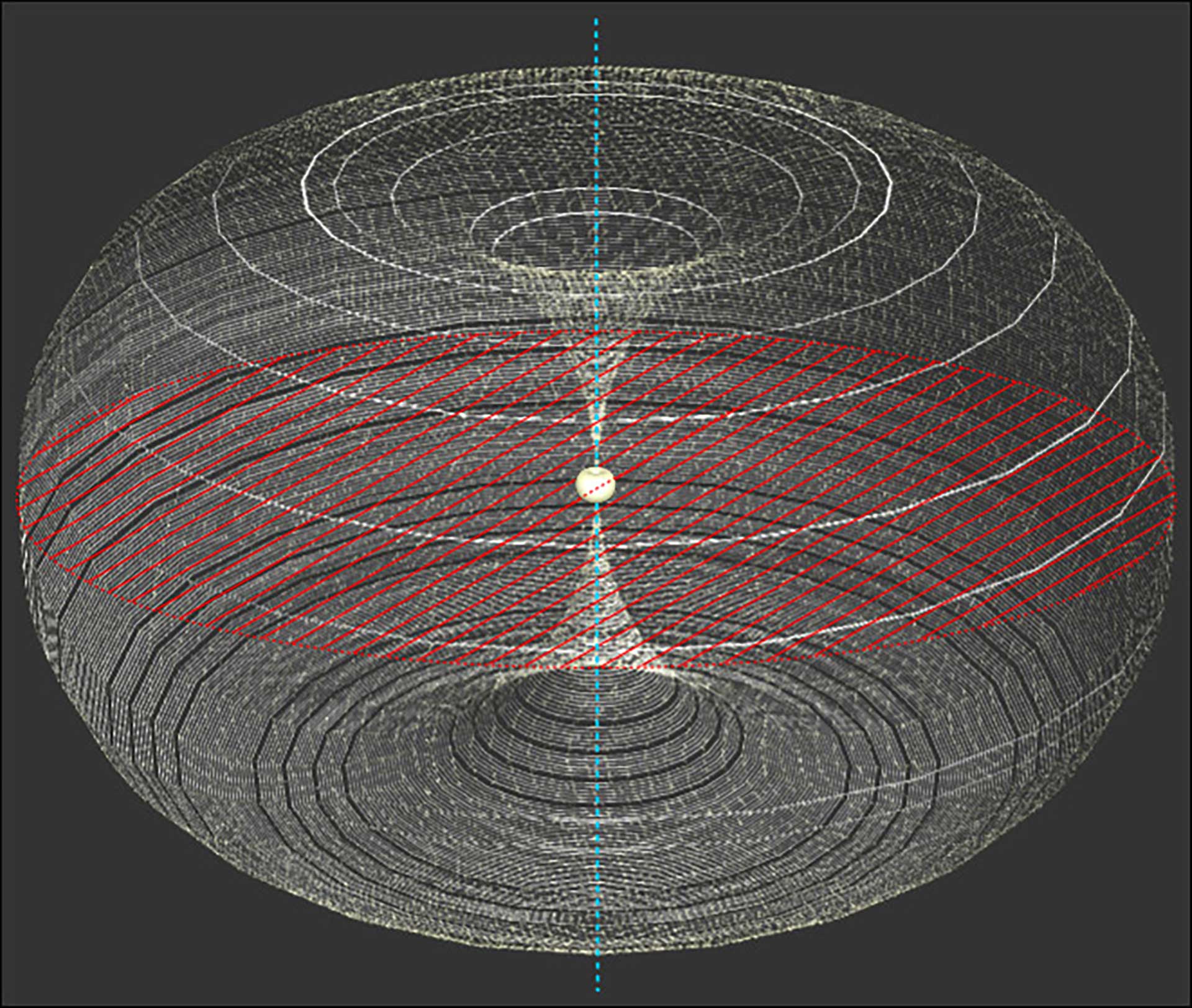
Abb. 3: Die Vorstellung des Schalenaufbaus des Atoms in Verbindung mit der Idee einer stehenden Welle führt zu einer schematischen Darstellung der
Elektronenschalen als liegende Achten als Querschnitt durch einen Torus.
Die schwarz gestrichelte Linie zeigt eine durch die Einfaltung der stehenden Welle entstehende polare Achse des Atoms. Die rot gestrichelten, äquatorialen Kreise deuten eine zur Polachse senkrechte Äquatorebene an.17
Stehende Welle
In der Berechnung der Größe des Universums auf maßstäblicher Ebene ergab sich eine Acht-Oktaven-Struktur. 5 Damit sich in einem unbegrenzten Raum eine stehende Welle herausbilden kann, ist von einem kreisförmigen Abschluss der 8-Oktaven-Struktur auszugehen. Bemerkenswerterweise findet sich nun im Schalenaufbau der Atome eine Oktavstruktur mit Atomkern und 7 Schalen. Betrachtet man diese als Schwingungsknoten, hat man es mit 8 an der Zahl zu tun. Die Überlegungen des kreisförmigen Abschlusses der Oktavenordnung der stehenden Schallwelle auf maßstäblicher Ebene in raum&zeit Nr. 221 führte dazu, anstelle der erforderlichen 9 Schwingungsknoten nur 8 anzunehmen, weil durch den Kreisschluss der 1. und der 9. Schwingungsknoten zusammenfallen und identisch sind.
Analog ist dies im Atomaufbau zu sehen, sodass der Atomkern als Zentrum den ersten und neunten Schwingungsknoten bildet. Zudem ist es erforderlich, dass Schale und Kern in widerklingender Verbindung stehen. Denkt man im Zweidimensionalen an einen Kreis, führt das Dreidimensionale zur Vorstellung eines kugelähnlichen Gebildes. Da man es aber nach hiesiger Annahme mit einem Hauptschwingungsknoten im Kern des Atoms zu tun hat, muss man neben einer kugelähnlichen Form von einer stehenden Welle zwischen innen und außen ausgehen; zwischen Schale und Kern bildet sich eine stehende Welle aus. Diese Überlegung führt zur Vorstellung einer Torusform (Abb. 3).
Die in Abbildung 3 gezeigten Elektronenschalen als liegende Achten ∞ repräsentieren mithin einen mittigen, senkrechten Schnitt durch das Atom. Je nach Energiemenge bildet sich eine kleinere oder größere Elektronenhülle als stehende, torusförmige Welle, die im Atomkern beziehungsweise am Äquator Anfang und Ende findet. Die Größe des Atomkerns ist in derselben Weise abhängig von der insgesamt vorhandenen Energie des betrachteten Atoms. Die unterschiedlichen Größen des Atoms bilden diskrete Werte in Übereinstimmung mit dem Oktavaufbau beziehungsweise dem 2n2-Gesetz, das Bohr bereits beschrieb. Die sogenannten gequantelten Energiemengen, die in der Quantenphysik erkannt wurden, haben ihre Ursache im Oktavaufbau.
Der Torus als stehende Welle ist demnach eine Abbildung des Ursprungs auf unterschiedlichen maßstäblichen Ebenen.
Kein Welle-Teilchen-Dualismus
Damit findet auch der Welle-Teilchen-Dualismus ein Ende, denn mit dieser Vorstellung lassen sich Elektronen als stehender Toruswellenwirbel erkennen, der in seinem Zentrum einen Körper, den Atomkern als Hauptschwingungsknoten verdichtend erzeugt. Da das Elektron den gesamten Wirbel der Atomhülle als stehende Welle darstellt, kann es auch nicht an einem bestimmten Punkt auf der Hülle bzw. auf einer Umlaufbahn geortet werden, wie es die Heisenbergsche Unschärferelation 6 zutreffend angibt.
Mit der Erkenntnis der Torusform lässt sich nachfolgend ein schlüssiges Bild eines Atoms zeichnen. Dazu der einfache Fall eines Protons: Ein torusförmiger Wirbel, der als Elektron bezeichnet wird, erzeugt in seinem Zentrum den Atomkern als maximale Verdichtung, die man Proton nennt (Abb. 4). Das Proton selbst ist auch torus- bzw. kugelförmig, je nach Energetisierungszustand und Umdrehungsgeschwindigkeit.
Die Torusform des Elektronenwirbels erlaubt ferner den Schluss, dass es die im Zentrum aufeinander treffenden Wirbelspitzen 7 sind, die das Proton als Kern bilden. 8 Je nach Energiezustand tritt der Toruswirbel als Elektron ohne Kern auf, man misst dann hinsichtlich Masse und Ladung ein Elektron, oder es liegt genügend Energie vor und das Elektron bildet ein Proton aus, das wesentlich komprimierter ist. Demnach kann man ein Proton mit einem hell strahlenden Sonnenstern vergleichen. So wird auch verständlich, warum Umfang und Radius eines Elektrons wesentlich größer sind, als die entsprechenden Werte des Protons. 9


Abbild des Ursprungs
Rückblickend auf die EINE Ursache von allem, die zuvor in Zusammenhang mit dem Oktavaufbau der Zahlen als stehende Welle beschrieben wurde, lässt sich unter Anwendung einer selbstähnlichen Sichtweise Folgendes erkennen: Wenn der atomare Aufbau dem Oktavaufbau folgt und in seiner Beschaffenheit als stehende Welle angelegt ist, ergibt sich daraus als mögliche Schlussfolgerung, dass das Atom in seinem grundlegenden Aufbau eine selbstähnliche Widerspiegelung der einen Ursache darstellt. Der Torus als stehende Welle ist demnach eine Abbildung des Ursprungs auf unterschiedlichen maßstäblichen Ebenen. Das materielle Universum selbst, aus seiner unbegrenzten Formlosigkeit entspringend – sein Ur-Sprung –, wäre damit nichts anderes als ein gigantischer Torus (Abb. 4).
Bemerkenswert ist in diesem Zusammenhang, dass die Form des Torus in sehr vielen natürlichen Strukturen ihre Widerspiegelung findet. Während man in Formen wie der des Wirbelsturms nur einen kleinen Teil eines Torus zu sehen bekommt, zeigen die Formen vieler Früchte, die uns ernähren und stärken, einen Torus (Abb. 5).
Im Übrigen wird daraus erkennbar, dass Atome eine vollständig elektrische Erscheinung darstellen. Damit gelangt man schließlich auch zu Walter Russells Darstellungen, der dieselbe atomare Form erkannte und von einem ausnahmslos elektrischen Universum sprach. 10
Der Gegenwirbel
Nun stellt sich noch die Frage, in welcher Richtung diese Toruswirbel rotieren. Dass sich der gesamte Toruswirbel nur in eine Richtung dreht, erscheint insofern unwahrscheinlich und auch unlogisch, als jede Bewegung einen Angriffspunkt braucht, der entsprechend Widerstand leistet, damit sich eine Bewegung anfänglich entwickeln kann. Da man es beim Atom mit einem in sich relativ abgeschlossenen System zu tun hat, dessen Architektur eine sich selbst begrenzende stehende Welle ist, braucht eine entstehende Umdrehungsbewegung nicht nur einen ruhenden Angriffspunkt, sondern erfordert zudem symmetrisch die Entstehung einer gleichförmigen entgegengesetzten Bewegung. Das bedeutet, man hat es im Kernzentrum mit zwei aufeinander treffenden, entgegengesetzt drehenden Wirbelspitzen zu tun. Die entgegengesetzte Umdrehung ist dafür verantwortlich, dass sich ein stark verdichteter Kern als Kugel oder Rotationsellipsoid herausbildet.
Die beiden entgegengesetzt drehenden Wirbel gehen von einer Äquatorebene aus, auf der eine ringförmige Erscheinung der Verdichtung entlang der Wirbelhülle (Edelgaszustand 11) auftreten kann. Diese ringförmige Verdichtung entsteht aufgrund derselben entgegengesetzten Umdrehung der Wirbel, die sich in ihrer Ausdehnung von der Äquatorebene hin zu den Polen nach innen einstülpen und den Kern bilden. Zwischen Kern, Äquator und schließlich wieder dem Kern bildet sich so eine stehende Welle heraus. Blickt man von außen in Richtung des Kerns, wird eine Art Strömungsrichtung des Wirbels entgegen des Uhrzeigersinns angenommen (Abb. 6). Abbildung 6 ist zu entnehmen, dass die toroidale Atomstruktur eine Nord-Süd-Polachse als Rotationsachse besitzt. Ferner zeigt sie nur eine Momentaufnahme des Protons in seinem Zustand maximaler Verdichtung. Denn die sogenannte Eigenschwingungsdauer eines Protons 12 entspricht seiner Lebensdauer zwischen Ausbildung zur vollständigen Kugel, seiner Auflösung und dem wieder Heranreifen zur vollständigen Kugelform; dies wurde vom Autor postuliert, Russell selbst geht darauf nicht genauer ein.
Wenn in Teil 2 die Steuerung der Atome beschrieben wird, kann der Leser noch besser nachvollziehen, warum es entgegen bisheriger Vorstellung von aneinandergedrängten Protonen und Neutronen Atomkerne nur in Form von Kugeln oder Rotationsellipsoiden oder sogar Atome als kernlose Toruswirbel gibt (Edelgase), deren Äquatorringe hauptsächlich verdichteter erscheinen. Der vielleicht staunende Leser möge sich in diesem Zusammenhang vor Augen halten, dass es mit gegenwärtigen Messmethoden noch zu beträchtlichen Fehlern kommen kann, wie in raum&zeit Nr. 227, S. 6 berichtet.
Der Toruswirbel besteht folglich aus zwei unterscheidbaren Wirbelelementen; der eine Teil ist der nach innen verdichtende, der andere Teil entdichtet den Kern und führt dagegen zu einer Dichtezunahme an den Äquatorringen. Dies erinnert stark an die beiden von Konstantin Meyl – er wies den skalaren Anteil der elektromagnetischen Schwingungen theoretisch und praktisch nach – unterschiedenen Wirbelformen des sogenannten starren Wirbels und Potentialwirbels.13 Fügt man also Meyls Wissen aus der Elektrotechnik hinzu, ist das Atom ein torusförmiger elektrischer Schwingkreis, der zwischen Potentialwirbel und starrem Wirbel hin- und herschwingt.
Fußnoten
1 Vgl. Pauqué, M. A. (2021): „Universelle Ordnung“. Band 1. Mathematische Grundlagen der Universellen Gleichmäßigkeit. Döbeln: Julia White Verlag; S. 123 f.
2 Lat. quantitas = die Menge
3 Siehe raum&zeit Nr. 221, S. 52 f.
4 Siehe raum&zeit Nr. 227, S. 63 f. und Fußnote 1: S. 146 f.
5 Siehe raum&zeit Nr. 221, S. 52 f.
6 Impuls-Ort-Beziehung: Δpx·Δx≥h/2π; Energie-Zeit-Beziehung: ΔE·Δt≥h/2π
7 Mit dem Begriff „Wirbelspitzen“ sind die trichterförmigen Einfaltungen an den Polen des in Abb. 4 dargestellten Torus gemeint.
8 So beschreibt auch Russell den Atomaufbau, vgl. Russell, W. und L. (2004). Fernstudienkurs Kosmisches Bewusstsein. Bremen: Genius Verlag, S. 445
9 Vgl. Fußnote 1: S. 130 f.
10 Vgl. Russell, W. (2019): „Eine neue Vorstellung vom Universum“. Bremen: Genius Verlag; S. 27 – Original: Russel, W. (1953): „A New Concept of the Universe“. Waynesboro: Walter Russell Foundation
11 Ebd.; S. 189
12 Vgl. Fußnote 1: 183 f.
13 Vgl. Meyl, K. (1990): „Über Wirbelphysik zur Weltgleichung“. Villingen-Schwenningen: Verlag INDEL GmbH; S. 12 f.
14 Vgl. Fußnote 1: S. 125
15 Ebd., S. 126
16 Ebd.; S. 127
17 Ebd.; S. 129
18 Ebd.; S. 130
19 Ebd.; S. 131
20 Ebd.; S. 133
Bildnachweis Einstiegsbild: © dani3315/AdobeStock


