Transformator konvertiert Raumenergie

Im Jahre 1831 beobachtete Michael Faraday, dass beim Ein- und Ausschalten des Stroms in einer Primärspule mit Eisenkern in der Sekundärspule eine Induktionsspannung entsteht. Die Urform des Transformators war gefunden. Transformatoren zum Umsetzen der verschiedensten Spannungen und Ströme sind in der Elektro- und Kommunikationstechnik sowie Elektronik heute unentbehrlich.

Ein Transformator wird meist mit Wechselstrom betrieben. Wechselstrom hat die „sanfteste“ Kurvenform: den Sinus. Dieser bewirkt im Quantenvakuum nichts. Soll im Quantenvakuum das Energie-Gleichgewicht verändert werden, so muss sehr schnell und extrem steilflankig geschaltet werden, andernfalls kommt es zu keinem Energie-Symmetrie-bruch und es reagiert nicht.

Welcher Effekt käme beim Transformator infrage, um die Vakuumenergie anzuzapfen? Ein interessanter Kandidat wäre die „Ferromagnetische Resonanz“. 1

Der Transformator-Konverter 

Bild 1 zeigt einen Transformator, bestehend aus einem ferromagnetischen Kern mit Primär- und Sekundärwicklung in Form von Kammerspulen. Der Kern besteht aus vier I-Stücken aus Mangan/Zink-Ferrit. Andere Kern-
geometrien wie Ringkern oder mit E-I-Schnitt sind ebenfalls möglich. Die Primär- und Sekundärwicklung sind hier doppeladrig einlagig gewickelt. Das Ende der Ader 1 wird mit dem Anfang der Ader 2 verbunden. Diese Beschaltung führt zu einem hohen Induktivitäts- und Kapazitätsbelag. Primär- und Sekundärspulen müssen in verschiedenen Kammern gewickelt werden. Sie dürfen nicht übereinander liegen, da sonst die magnetische Kopplung zu fest ist. Die Wicklungen hier hatten ein Übersetzungsverhältnis von 1:1 und je 30 doppeladrige Windungen. Andere Übersetzungsverhältnisse und Windungszahlen sind natürlich auch möglich.

In Bild 2 sehen wir die Schaltung für den Versuchsaufbau zur messtechnischen Überprüfung seiner Funktion und in Bild 3 den realen Aufbau des Versuchs mit Transformatorkern (TK) und Messgeräten. Als Messgeräte kommen zum Einsatz: a) ein Funktionsgenerator als Signalquelle; b) ein Mehrkanal-Oszillograph zur Darstellung der Messkurven für den Ein- und Ausgang des Konverters; c) ein Differenz-Tastkopf zur genauen Messung der Ströme.

Etwas Besonderes ist die Signalquelle. Sie muss Spannungen abgeben, die die Form eines gleichschenkligen Dreiecks haben. Die Grundseite (Zeitachse) dieser gleichschenkligen Dreiecke muss veränderbar sein, ebenso die Wiederhol-Frequenz der Dreiecksspannungspulse.

Man kann auch mit preisgünstigen Funktionsgeneratoren in guter Näherung die gewünschte Dreiecksform der Pulse einstellen. Man stellt die Funktion „Rechteck“ ein und geht mit dem Tastgrad2 (engl. Duty Cycle) unter 1 Prozent. Die preiswerteren Geräte können zwar im Hochfrequenzbereich meist kein sauberes Rechteck-Signal mehr erzeugen; in guter Näherung kommt ein gleichschenkliges Dreieck zustande (Bild 4). Ideal ist das nicht, aber für erste Versuche ausreichend.

Ich messe Ströme im Hochfrequenz-Bereich nur noch über die Heiße Ader zwischen dem Funktionsgenerator und dem TK-Eingang mittels eines Differenz-Tastkopfes über einen kleinen Vorwiderstand R_v von 10 Ohm. So werden Amplituden- und Phasenfehler vermieden. Von der gebräuchlichen Messmethode, über einen 1 Ohm-Widerstand in der Masseleitung indirekt den Strom zu messen, rate ich ab, weil gerade im Hochfrequenz-Bereich die Masse „verschleift“ und „Vagabundierende Hochfrequenz“ unklare Messergebnisse produziert.

Wirkleistung am Ausgang

Der TK nimmt keine Wirkleistung bei bestimmter Form der Eingangsspannung und des -stromes auf; dagegen Pendelleistung (Blindleistung) schon. Die Energie, die innerhalb einer Sequenz – von Dreiecksspannungspuls zum folgenden Dreiecksspannungspuls  – ausgehend von der Quelle in den TK hineinfließt, fließt auch in gleicher Menge aus dem TK wieder heraus und zurück zur Signalquelle, sodass seine Wirkleistungsaufnahme = 0 ist. Das Interessante ist, dass er Wirkleistung am Ausgang an den elektrischen Verbraucher abgibt. Wo kommt diese Energie her? Ich gehe davon aus, dass diese Energie aus dem Vakuum stammt. Dieser Effekt entsteht im nichtlinearen Teil des ferromagnetischen Kernmaterials.

Zur optimalen Wandler-Funktion müssen zwei Resonanzen in Beziehung gebracht werden: a) Die Eigenresonanz des Transformators; sie wird durch die Primär-/Sekundärspule mit ihren Induktivitäts- und Kapazitätsbelägen sowie der Permeabilität des ferromagnetischen Kerns bestimmt. b) Die Ferromagnetische Resonanz der Elementarmagnete des ferromagnetischen Materials.

Ferromagnetische Resonanz

Es gibt spezielle Bedingungen, unter denen Energie aus den Quantenfluktuationen des Vakuums gewonnen werden kann. Dieser Mechanismus basiert auf Ferromagnetischer Resonanz. Hierbei tauschen die freien Elektronen Energie mit virtuellen Elektronen des Vakuums aus. Normalerweise ist dieser Austausch symmetrisch. Es bleibt beim Energie-Gleichgewicht und keine reale Energie entsteht. In der Quantenmechanik können keine zwei Elektronen den gleichen Zustand haben. 

Die Ferromagnetischen Resonanzen liegen in einem breiten Band hoher Frequenzen. Der Effekt der Energieauskopplung funktioniert nur im nichtlinearen Teil der Hysterese-Kurve des ferromagnetischen Materials. Mit zunehmendem Stromanstieg in der Primärspule des TK vermindert sich der Induktivitätszuwachs und mit kleiner werdendem Stromanstieg vergrößert sich der Induktivitätszuwachs in der Primärwicklung des TK. Das ist das nichtlineare Verhalten des ferromagnetischen Kerns.3

Negative Permeabilität

Der starke Strom in der Primärspule kommt einer Elektronen-Lawine gleich. Während dieser Zeitspanne wird Energie aus dem Quantenvakuum aufgenommen. Der Verlauf der Permeabilität ist negativ. Das heißt, dass ein Negativer Differentieller Magnetischer Widerstand vorliegt und Energie aus dem Quantenvakuum entnommen wird. In der Zeitspanne mit vermindertem Eingangsstrom erhöht sich der Induktivitätszuwachs wieder. Dabei wird keine Energie aus dem Quantenvakuum entnommen. Entscheidend ist noch zu vermerken, dass diese Zeitspanne kürzer ist als die Erstere. 

Der oben beschriebene Ablauf wird mit jedem Eingangspuls neu gestartet. Die Wiederhol-Frequenz der Dreieckspulse ist gleich der Eigenresonanz-Frequenz des TK. Der Anregungspuls für die reale sinusförmige Leistungsabgabe des TK ist der gleichschenklige Dreiecksspannungspuls mit seinem sinusförmig verlaufenden Strom am Eingang des TK, der keine Wirkleistung enthält. 

Anders ausgedrückt: Der TK gibt auf der tiefen Frequenz, der Eigenresonanz-Frequenz, eine Sinusschwingung an seinem Ausgang als reale Leistung an den Verbraucher ab. Die schmalen Ansteuerimpulse bestimmter Form müssen steile Anstiegs- und Abfallflanken in ihrem Formationskollektiv haben. Nur so ist ein asymmetrischer Energieaustausch durch einen Energie-Symmetriebruch im Quantenvakuum möglich. In diesem Fall wird reale Energie aus dem Quantenvakuum gewonnen!

Der Pendelstrom zwischen der Signalquelle und dem TK-Eingang fließt auch durch den in Reihe liegenden Innenwiderstand der Signalquelle. Dieser Widerstand ist ohmscher Natur und verbraucht reale Leistung. Diese Wirkleistung kommt aus dem Generator selbst und errechnet sich mit dem Ausgangsstrom der Quelle (auch Eingangsstrom des TK) zum Quadrat mal dem Innenwiderstand der Signalquelle. 

Es muss darauf geachtet werden, dass der Innenwiderstand der Signalquelle sehr klein ist. Nur dann sind die realen Verluste in der Signalquelle selbst auch sehr klein und fallen bei der Gesamtsystem-Betrachtung nicht ins Gewicht.

Unser Ziel muss sein, den TK so einzustellen, dass mehr elektrische Leis-tung und damit Energie herauskommt, als hineingesteckt wird. Das Verhältnis Ausgangswirkleistung/Eingangswirkleistung ist die Leistungsziffer, auch Leistungszahl genannt. Im Englischen ist es der Coefficient of Performance (COP).

Ermitteln der Leistungsziffer

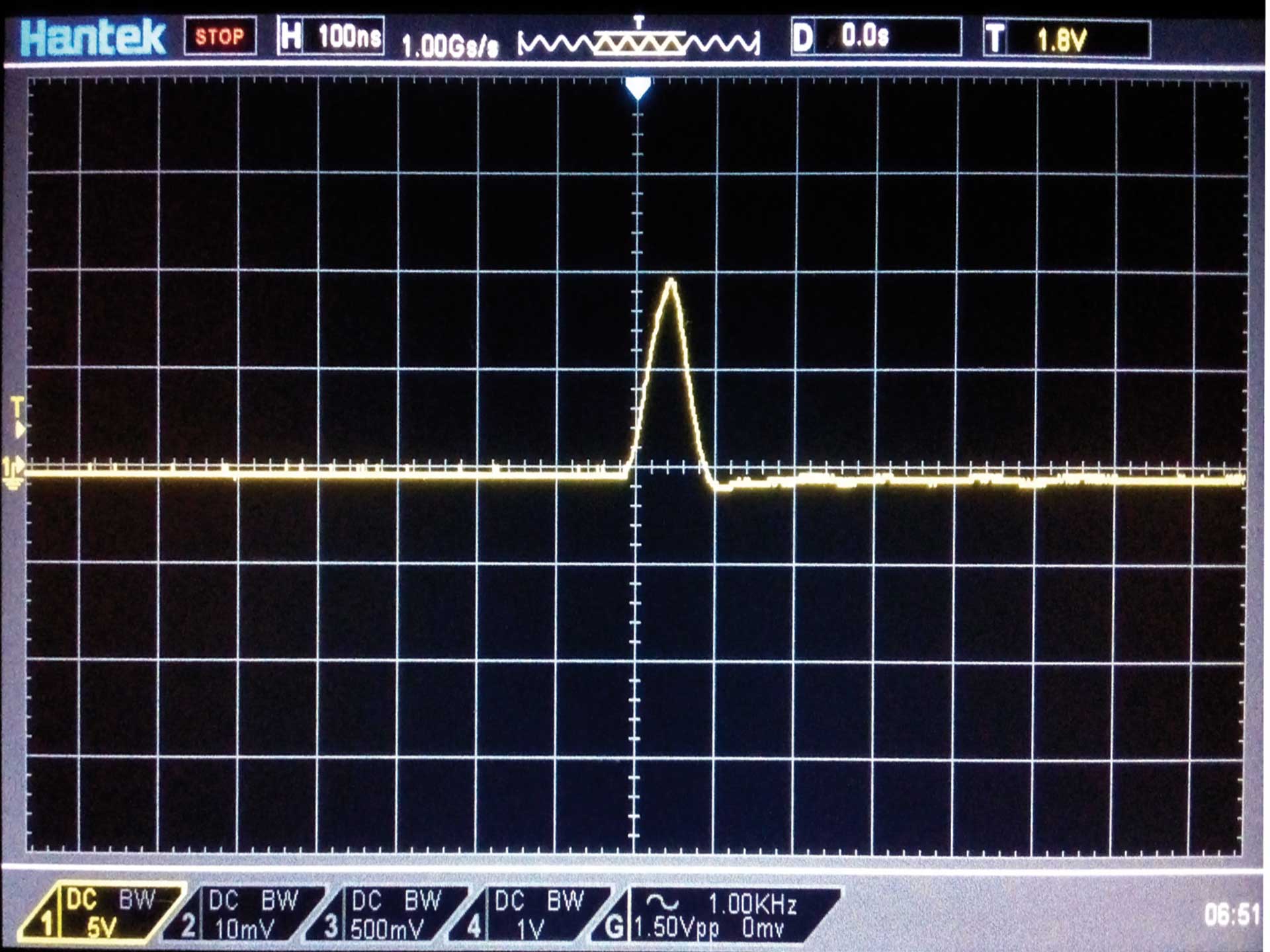
Wir müssen beim TK das optimale gleichschenklige Spannungsdreieck und den optimalen sinusförmigen Eingangsstrom einstellen (Bild 5). Beide Optima erreichen wir mit der „Rechteckfunktion“ und einem Duty Cycle von unter 1 Prozent. Die Grundseite dieses Spannungsdreiecks ist dann Teil der Zeitachse des Oszillographenschirms. Das dreiecksförmige Spannungssignal legen wir auf Kanal 1 des Oszillographen. Das ist auch unser Triggersignal (Anschlüsse C/D in Bild 2).

Der sinusförmige Eingangsstrom des TK fließt vom Funktionsgenerator kommend über einen 10 Ohm Vorwiderstand R_v der heißen Ader zwischen Funktionsgenerator und TK. An den Anschlüssen des Messwiderstands klemmen wir den Differential-Tastkopf an (Anschlüsse A/C in Bild 2) und geben das Signal weiter auf Kanal 2 des Oszillographen. So messen wir indirekt den Eingangsstrom des TK. Falls der sinusförmige Eingangsstrom nicht die Zeitachse des Oszillographenschirms spiegelsymmetrisch schneidet, korrigieren wir das mit einem entsprechenden Offset des Funktionsgenerators (Bild 5).

Der Eingangsstrom des TK hat hier eine Periodenlänge von 95 Nanosekunden. Bei dieser Periodenlänge ist in diesem Fall die Sinusform des Eingangsstroms optimal abgebildet. Das entspricht einer Frequenz von 10,563 Megahertz. Im Idealfall ist die Periodenlänge des Eingangsstromes genauso lang wie die Basisseite des gleichschenkligen Eingangsspannungsdreiecks.

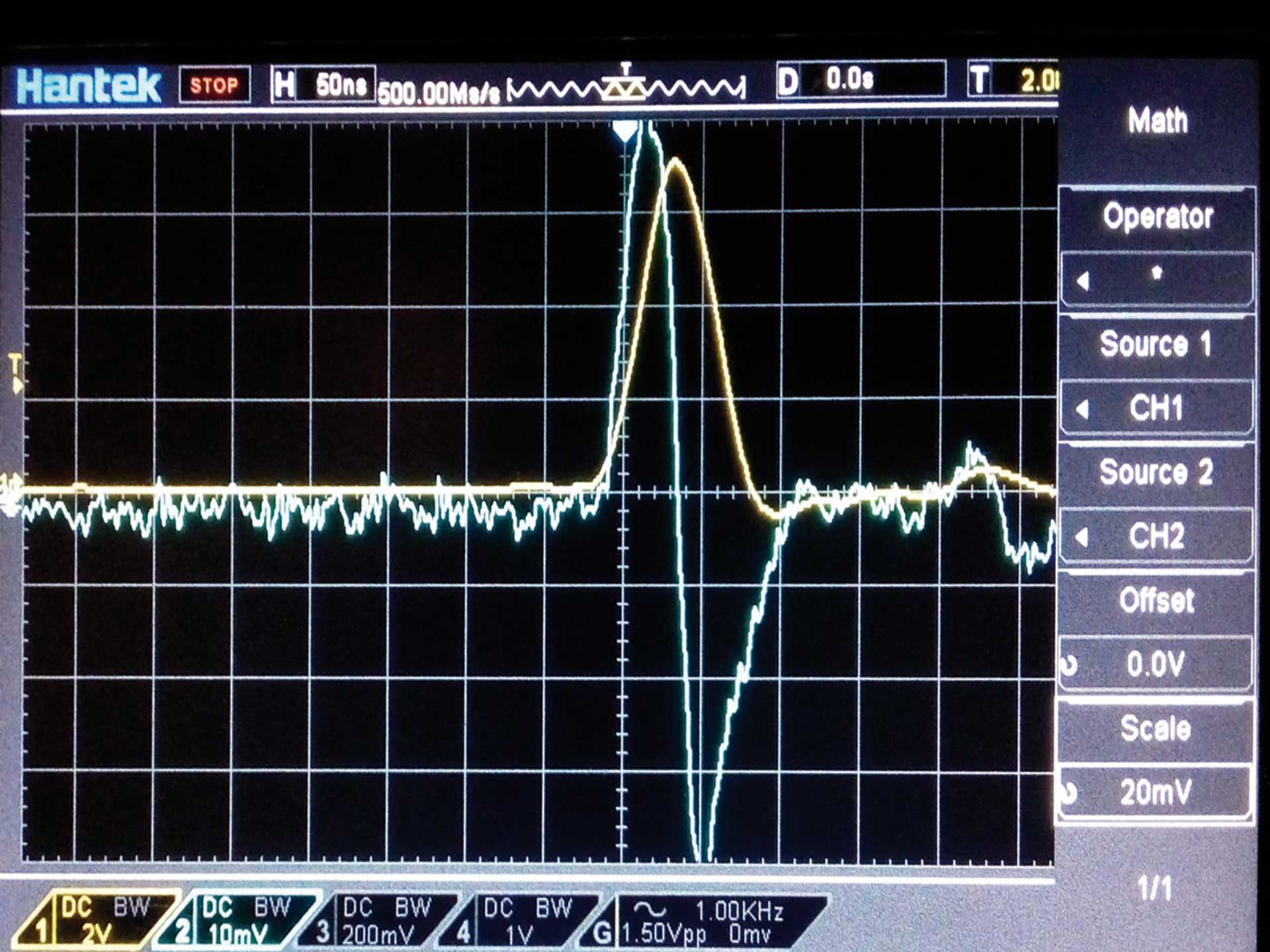
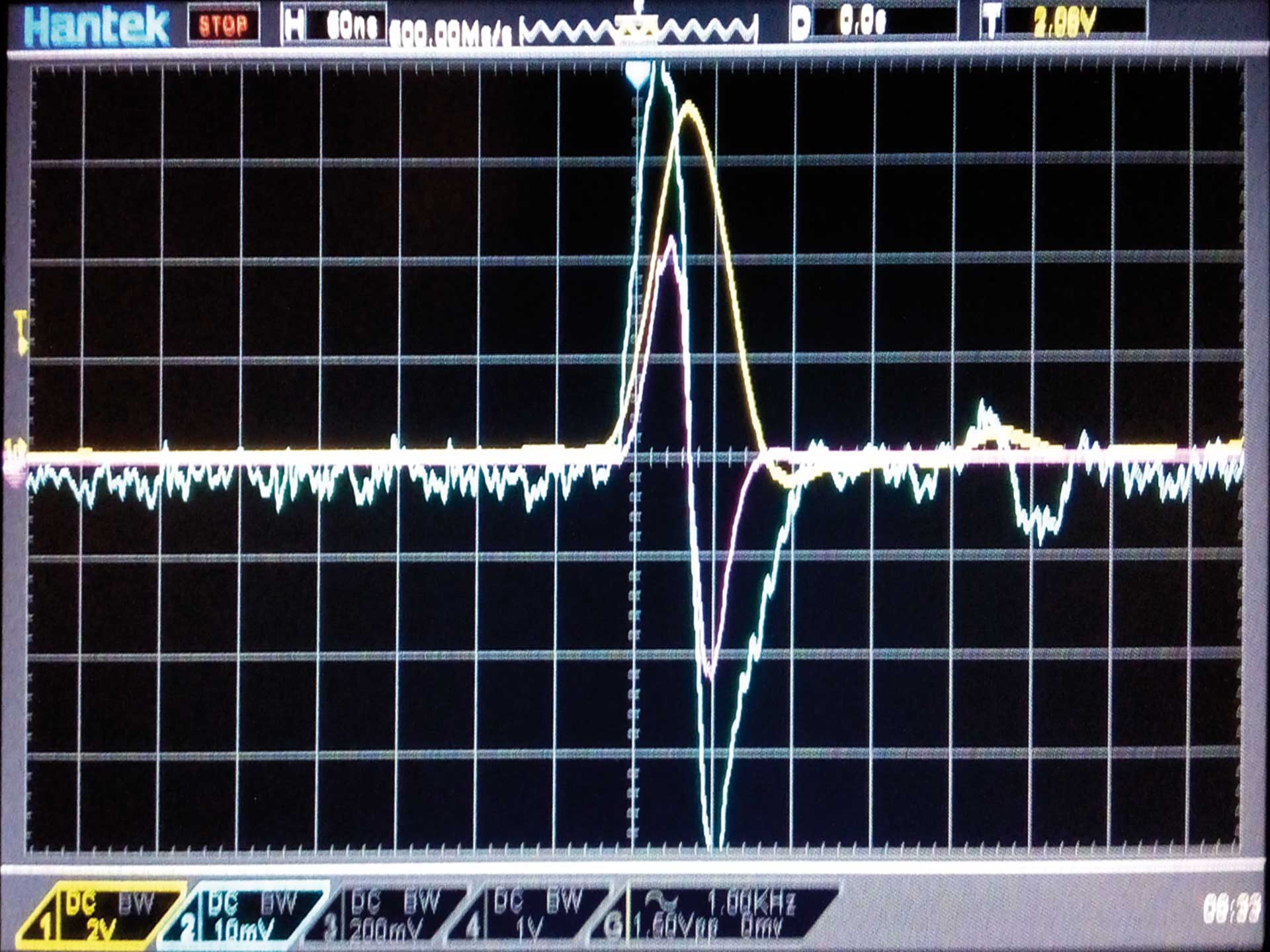
In Bild 6 wird mit der Mathematik-Funktion des Oszillographen zu der Eingangsspannung (gelb) und dem Eingangsstrom (blau) eine dritte Kurve hinzugefügt. Es ist die Eingangsleistungskurve (lila) des TK. Diese pendelt zwischen einer maximalen positiven Amplitude und einer gleich großen negativen Amplitude spiegelsymmetrisch um die Zeitachse des Oszillographenschirms. Das heißt, dass innerhalb der Eingangsleistungsperiode im Mittel die Leis-tung 0 ist. Im restlichen Teil der zeitlichen Sequenz ist sie ebenfalls 0, weil weder Eingangsspannungen noch -ströme vorhanden sind. Innerhalb der Sequenz, also von Eingangsspannungspuls zu Eingangsspannungspuls ist die Leistungsaufnahme 0. Der TK nimmt keine Eingangswirkleistung auf. Wenn er Wirkleis-tung aufnehmen würde, so würde die Leistungskurve oberhalb oder auch unterhalb der Zeitachse liegen; doch das tut sie nicht. Sollte außerhalb der Spannungs-Dreiecke ein Resteingangsstrom vorhanden sein, so ist das unbedeutend, weil außerhalb der Spannungsdreiecke die Eingangsspannung 0 ist und damit ist auch die Eingangswirkleistung 0.

Falls die mittlere Eingangsleistung nicht 0 ist, müssen wir den Offset des Funktionsgenerators so verstellen, dass sie 0 ist. Durch den Offset optimieren wir die Arbeitspunkt-Einstellung im ferromagnetischen Kern. Im Idealfall ist die Basisseite des gleichschenkligen Eingangsspannungsdreiecks gleich der Periodenlänge des Eingangsstromes und der Periodenlänge der Eingangsblindleistung (Eingangspendelleistung).

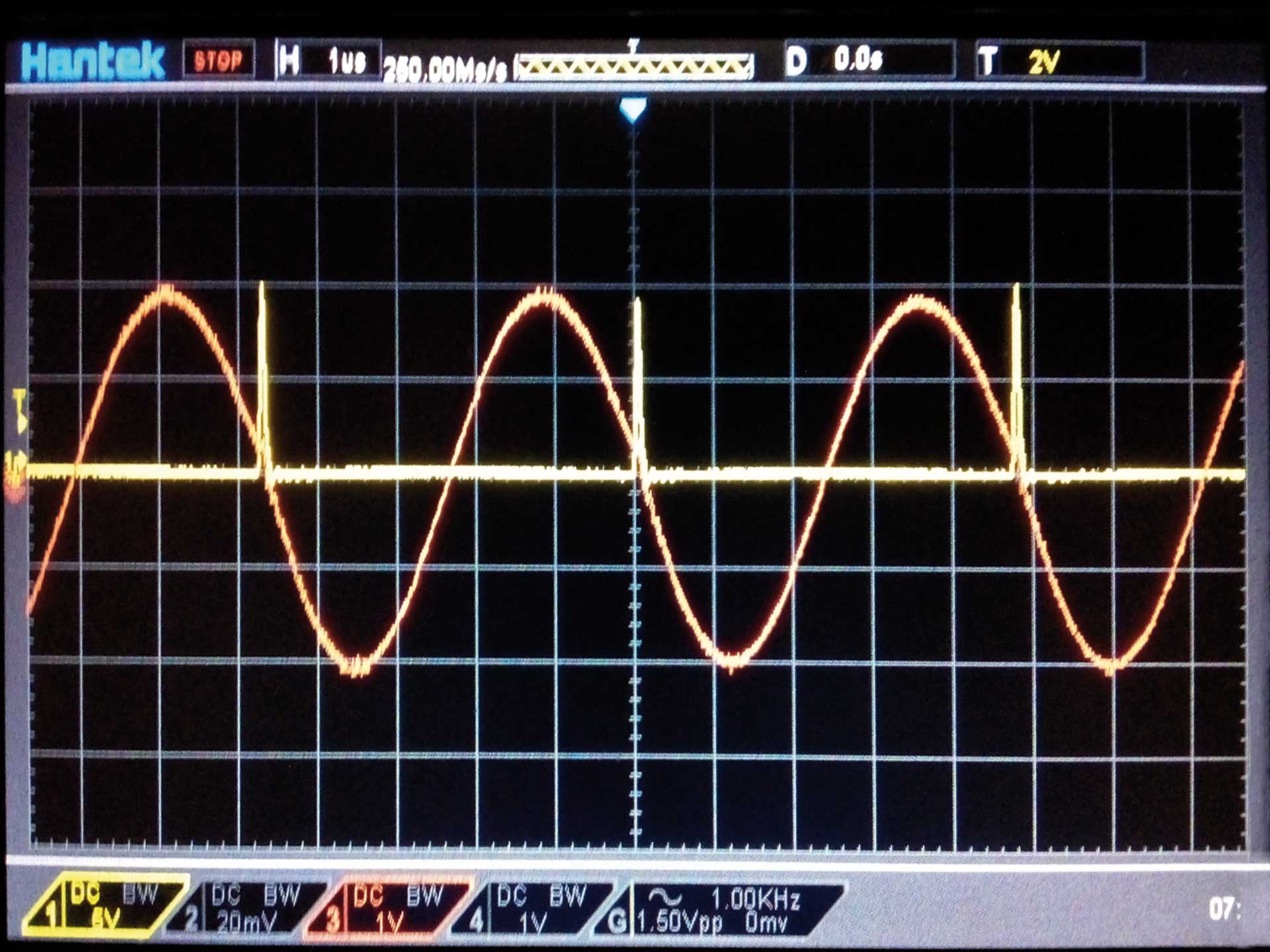
Auf Kanal 1 des Oszillographen lassen wir wegen der Triggerung den Spannungsdreieckspuls geschaltet. Auf Kanal 2 legen wir den Ausgang des TK (Anschlüsse E/F in Bild 2). Wir messen also die Ausgangsspannung über dem Verbraucherwiderstand von RLast = 20 Kilo-Ohm des TK (rote Kurve in Bild 7). Werden mehr als eine Sinusschwingung bei der Ausgangsspannung auf dem Oszillographenschirm gezeigt, so haben wir zwei Möglichkeiten zur Darstellung von nur einer Sinusschwingung: Wir schalten parallel zum TK-Ausgang einen Drehkondensator und machen eine Feinabstimmung oder wir erhöhen die Windungszahl der Sekundärwicklung. In beiden Fällen wird der Ausgangsparallelschwingkreis auf die optimale Resonanzfrequenz abgestimmt. Die Ausgangsspannung beträgt hier 2 Volt effektiv bei Leistungsanpassung und einer Eigenresonanzfrequenz von 208,333 KHz.

Die Ausgangswirkleistung bei Anpassung (halbe Ausgangsleerlaufspannung) errechnen wir gemäß der Formel (U_Ausgang)2/R_Last. Sie beträgt 0,2 mW. Die Ausgangswirkleistung des TK ist zwar endlich und hängt von verschiedenen Parametern des TK ab; doch der COP strebt gegen unendlich, weil die Eingangswirkleistung 0 ist. Sie versinkt im Rauschen. COP = Ausgangswirkleistung/Eingangswirkleistung = 0,2 mW/0 mW = unendlich. Der Wert der Ausgangswirkleis-tung ist zwar klein; aber über dem Rauschen noch deutlich messbar!

Wesentliche Einflussfaktoren beim TK sind: a) Verwendetes ferromagnetische Kernmaterial; b) Kernverluste; c) Übersetzungsverhältnis von Primärspule zur Sekundärspule; d) Verluste in den Spulen; e) Drahtstärken der Spulen; f) Eigenresonanzfrequenz des TK; g) Geometrische Abmessungen und Form des TK; h) Eingangsspannung und deren Abweichung von der Form eines gleichschenkligen Dreiecks; i) Arbeitspunkt-Einstellung. Sämtliche Einflussfaktoren müssen optimal aufeinander abgestimmt sein.

Fazit

Das bisher Erreichte ist nur ein Anfang. Die eigentliche Entwicklungsarbeit beginnt erst. Bisher wurde nur festgestellt, dass es einen physikalisch-technischen Effekt auch bei Transformatoren gibt, der die Wandlung der Vakuumenergie in reale Energie ermöglicht. Dieser Effekt ist messbar und er darf daher nicht vernachlässigt werden. Er tritt bei verlustarmen Transformatoren mit ferromagnetischen Kernen auf. Ein Einsatz mit mehreren Kernschenkeln und daher Phasen ist bei entsprechender Pulsform und dem passenden Puls-Kollektiv durchaus realisierbar. Bis es zu praxisnahen Produkten kommen könnte, ist noch umfassende Entwicklungsarbeit zu leisten.

Das Einsatzfeld des TK ist nach erfolgter Optimierung sehr groß. Er könnte in Lampen, Radiatoren, TV-und Haushaltsgeräten direkt integriert werden. Wir bräuchten im Haus keine Steckdosen mehr und der Öffentliche Stromanschluss oder die Solaranlage auf dem Dach wären obsolet. Bei entsprechender Größe der TK könnten auch Autos, Lokomotiven, Schiffe, Flugzeuge etc. angetrieben werden. 

Sämtliche Baukomponenten des TK sind verfügbar. Mit modernen schnellen Halbleitern können die gewünschten steilflankigen Spannungsdreieckspulse realisiert werden. Marktgängig sind auch die fast verlustlosen ferromagnetischen Kernwerkstoffe mit eng verlaufender und eckiger Hystereseschleife. Transformatoren sind heute preiswerte Massenprodukte, die wir in einer Vielzahl sehr verschiedener Geräte finden. Da der TK einfach herzustellen ist, könnte er ein preiswertes Massenprodukt werden. Gewiss, es gibt noch weitere Effekte, um die Energie des Vakuums in reale Energie zu wandeln; aber in Anbetracht seiner Einfachheit ist der TK kaum zu überbieten.

Jeder Experimentator muss wissen, dass bereits bei kleinen Ausgangsleis-tungen gefährliche Resonanzspannungen im Wandler selbst entstehen können. Weder der Verlag noch der Autor übernehmen die Verantwortung beim Experimentieren mit hohen Resonanzspannungen. Aus Sicherheitsgründen ist es ratsam, entstehende Torsionsfelder 4 durch ein Gehäuse aus Aluminium abzuschirmen

Bildnachweis Einstiegsbild: © fotoplot/Adobe Stock